Олимпиада по начертательной геометрии 2019

          Начертательная геометрия по своему содержанию занимает особое положение среди других наук: она является лучшим средством развития у человека пространственного воображения, без которого немыслимо никакое инженерное творчество.

                                  Академик Российской Академии проблем качества, заслуженный деятель науки и техники РСФСР, профессор Фролов С.А.

 20 декабря 2019 г. состоялась Олимпиада по начертательной геометрии среди студентов младших курсов на основе общеобразовательной программы по начертательной геометрии для технических вузов (согласно Положению об Олимпиаде-2019 по начертательной геометрии). В соревновании приняло участие более 150 студентов.

Победители:

1 место (40 баллов) -  Бельшева Мария, группа БМТ1-11Б

2 место (38 баллов) - Бутрим , группа МТ7-12

3 место (32 балла) - Попов Максим и Земцов Артём, группа СМ7-14Б; Корсаков Александр , группа РЛ1-11

 Победители, призеры и получившие по результатам Олимпиады 75% и более от максимальной оценки имеют право на получение досрочной экзаменационной оценки по начертательной геометрии - "отлично", получившие оценку 65-74% от общей максимальной оценки - "хорошо". При этом, студент должен сдать при оформлении экзамена все выполненные семестровые работы и рабочие тетради к лекциям и практическим занятиям преподавателю, оформляющему экзамен. (Положение об Олимпиаде-2019 по начертательной геометрии).

Оргкомитет Олимпиады-2019.

РЕШЕНИЕ ЗАДАЧИ 1

РЕШЕНИЕ ЗАДАЧИ 2

РЕШЕНИЕ ЗАДАЧИ 3

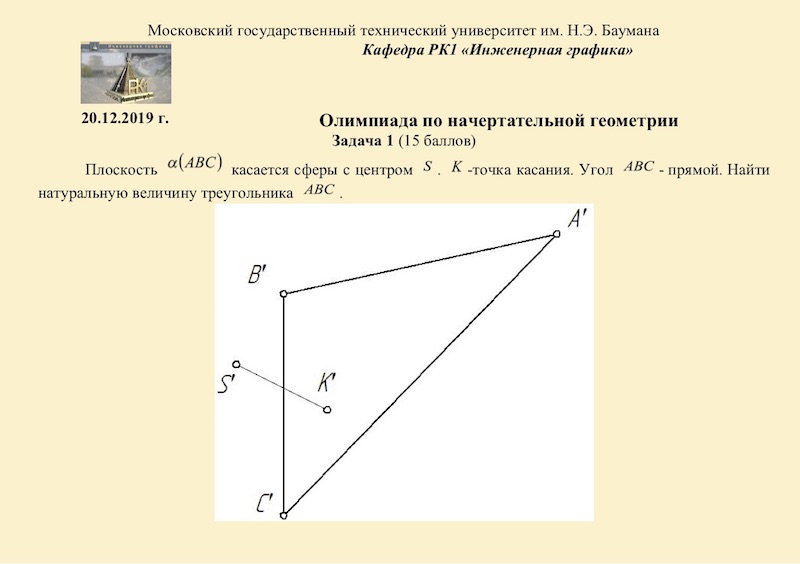
Литература для подготовки:

1.  Материалы для подготовки к Олимпиаде - Иванов Г.С., Серегин В.И., Боровиков И.Ф. (Скачать 1,7 МБ)

2.  Иванов Г.С. Начертательная геометрия. – М.: Изд-во МГУЛ, 2012. – 340 с.        

3.  Пеклич В.А. Задачи Московских и всероссийских олимпиад по начертательной геометрии  – М.: Изд-во Ассоциации строительных вузов, 2003. – 156 с.

4. Пеклич В.А. Начертательная геометрия – М.: Изд-во Ассоциации строительных вузов, 2007. – 248 с. (Библиотека МГТУ им. Н.Э.Баумана)

5. Пеклич В. А., Жирных Б. Г., Марков В. М. Задачи московских и российских олимпиад по начертательной геометрии  - М. : Изд-во Ассоциации строит. вузов, 2004. - 156 с.  (Библиотека МГТУ им. Н.Э.Баумана)

Олимпиада по начертательной геометрии 2018 

Олимпиада по начертательной геометрии 2017 

Олимпиада по начертательной геометрии 2016 

Олимпиада по начертательной геометрии 2015

Олимпиада по начертательной геометрии 2014